AlgorithmsGreedy Approach

Minimum Spanning Trees - Kruskal's Algorithm(최소신장트리-크러스컬)

알고리즘, 최소신장트리, 탐욕알고리즘

We will investigate two different greedy algorithms for minimum spanning trees, Prim’s algorithm and Kruskal’s algorithm. Each uses a different locally optimal property.

프림 알고리즘 대신 크러스컬 알고리즘을 이용해도 최소신장트리를 구할 수 있다.

Example Determine a minimum spanning tree.


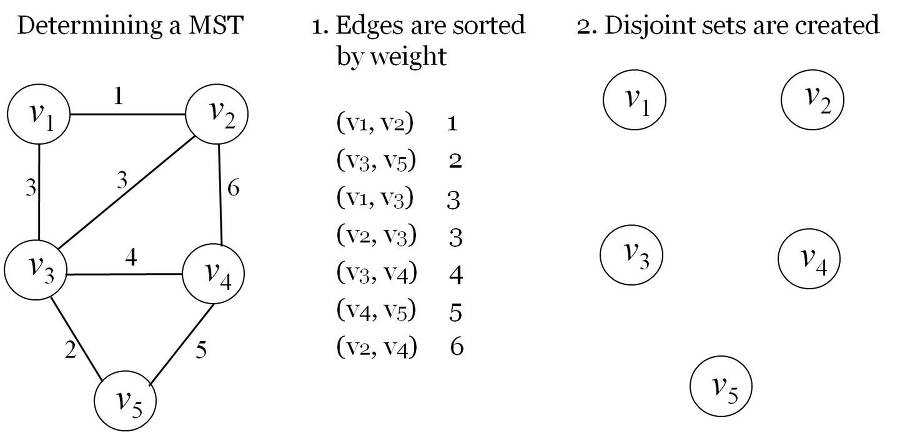
Step 1 가중치를 기준으로 전체 이음선들을 오름차순으로 정렬한다.

Step 2 5개의 정점들이 있으므로 총 5개의 서로소 집합, 즉 {$v_1$}, {$v_2$}, {$v_3$}, {$v_4$}, {$v_5$}이 만들어지게 된다.

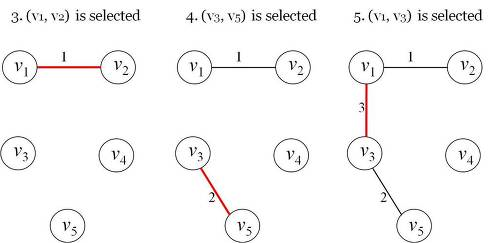
Step 3 오름차순으로 정렬된 이음선 중 최소가중치 값인 1이 선택된다. 1은 $v_1$정점과 $v_2$정점을 연결해주는 이음선 값이다. 그리고 $v_1$과 $v_2$는 서로소 집합이므로 두 집합을 하나의 부분집합으로 합진다. 현재까지의 부분집합은 {$v_1$, $v_2$}, {$v_3$}, {$v_4$}, {$v_5$} 이렇게 4개이다.

Step 4 최소가중치를 갖는 이음선으로 $v_3$정점과 $v_5$정점을 연결해주는 2가 선택된다. $v_3$과 $v_5$역시 서로소 집합이므로 두 집합을 하나의 부분집합으로 합친다. 현재까지의 부분집합은 {$v_1$, $v_2$}, {$v_3$, $v_5$}, {$v_4$} 이렇게 3개이다.

Step 5 최소가중치를 갖는 이음선으로 $v_1$정점과 $v_3$정점을 연결해주는 3이 선택되며, 위의 과정이 똑같이 수행된다. 현재까지의 부분집합은 {$v_1$, $v_2$, $v_3$, $v_5$}과 {$v_4$} 이렇게 총 2개이다.

Step 6 다음으로 $v_2$정점과 $v_3$정점을 연결해주는 이음선 3이 선택된다. 그러나 $v_2$와 $v_3$의 경우 이미 같은 집합에 포함되어 있다. 같은 집합의 정점들끼리 연결하는 경우에는 순환경로가 생기므로 $v_2$정점과 $v_3$정점을 연결하는 이음선은 버린다.

Step 7 마지막으로 $v_3$정점과 $v_4$정점을 연결하는 이음선이 선택되고, 5개로 출발했던 서로소 집합들이 하나의 집합으로 합쳐졌기 때문에 최소신장트리가 완성된다.


Kruskal’s Algorithm

Algorithm Design

To write a formal version of Kruskal’s algorithm, we need a disjoint set abstract data type. The disjoint set abstract data type consists of data types index and set pointer, and routines initial, find, merge, and equal.

크러스컬 알고리즘에서는 서로소 집합(disjoint set)의 자료구조가 사용된다.

Kruskal’s algorithm for the Minimum Spanning Tree problem starts by creating disjoint subsets of V, one for each vertex and containing only that vertex. It then inspects the edges according to nondecreasing weight (ties are broken arbitrarily). If an edge connects two vertices in disjoint subsets, the edge is added and the subsets are merged into one set. This process is repeated until all the subsets are merged into one set. The following is a high-level algorithm for this procedure.

정점들의 개수 만큼 서로소 부분집합을 생성하고, 가중치를 기준으로 전체 이음선들을 오름차순으로 정렬한다. 그 다음 오름차순으로 정렬된 이음선들을 하나씩 조사하면서, 해당 이음선이 연결하고 있는 정점들이 서로소 부분집합이면 두 개의 부분집합을 하나로 합친다. 이 과정을 모든 서로소 부분집합들이 하나의 집합으로 합쳐질 때까지 계속 수행한다.

Pseudo Code

void kruskal(int n, int m, set_of_edges E, set_of_edges& F)
{
  index i, j;
  set_pointer p, q;  
  edge e;

  Sort the m edges in E by weight in nondecreasing order;
  F = "empty";
  initial(n);

  while (number of edges in F is less than n-1)
  {
    e = edges with least weight not yet considered;
    i, j = indices of vertices connected by e;
    p = find(i);
    q = find(j);
    if (!equal(p,q))
    {
      merge(p,q);
      add e to F;
    }
  }
}

Source Code

// File: kruskal.h
#ifndef KRUSKAL_H
#define KRUSKAL_H
#include <string>
#include "graph.h"
using namespace data_structures;

namespace algorithms
{
  struct edge
  {
    std::string vertex[2];
    int weight;
  };
  typedef struct edge edge;
  typedef edge* set_of_edges;

  void kruskal(int n, int m, set_of_edges& E, set_of_edges& F);
  // Problem: Determine a minimum spanning tree.
  // Inputs: integer n >= 2, positive integer m, and a connected, weighted,
  // undirected graph containing n vertices and m edges. The graph is
  // represented b y a set E that contains the edges in the graph along
  // with their weights.
  // Outputs: F, a set of edges in a minimum spanning tree.

  void make_edgeset(const graph g, set_of_edges& E, int& num_of_edges);
  void init_edgeset(set_of_edges& F, const int n);

  void mergesort2(set_of_edges& data, int low, int high);
  void merge2(set_of_edges& data, int low, int mid, int high);
  }

#endif
// File: kruskal.cpp
#include <string>
#include "disjointset.h"
#include "kruskal.h"

namespace algorithms
{
  void kruskal(int n, int m, set_of_edges &E, set_of_edges &F)
  {
    disjointset dsjset(n); // disjoint set
    disjointset::index i, j;
    disjointset::set_pointer p, q;
    edge e;

    // Sort the m edges in E by weight in nondecreasing order
    mergesort2(E, 0, m);

    dsjset.initialize(n); // Initialize n disjoint subsets.

    int k = 0;
    int repeat = 0;
    while (repeat < n)
    {
      // edge with least weight not yet considered
      e.weight = E[repeat].weight;
      e.vertex[0] = E[repeat].vertex[0];
      e.vertex[1] = E[repeat].vertex[1];

      // indices of vertices connected by e
      i = atoi(e.vertex[0].c_str());
      j = atoi(e.vertex[1].c_str());
      p = dsjset.find(i);
      q = dsjset.find(j);

      if (!dsjset.equal(p, q))
      {
        dsjset.merge(p, q);
        F[k++] = e;
      }
      ++repeat;
    }
  }

  void make_edgeset(const graph g, set_of_edges &E, int &num_of_edges)
  {
    edge e;
    int cnt = 0;
    int k = 0;

    for (int i = 1; i <= g.get_size(); ++i)
    {
      for (int j = i; j <= g.get_size(); ++j)
      {
        if (g.get_edge(i, j) != graph::INFINITE && g.get_edge(i, j) != 0)
        {
          // edge connecting vertices index by i and j
          e.vertex[0] = std::to_string(i);
          e.vertex[1] = std::to_string(j);
          e.weight = g.get_edge(i, j);

          E[k++] = e; // add e to E
          ++cnt;    // count valid edges
        }
      }
    }

    num_of_edges = cnt;
  }

  void init_edgeset(set_of_edges &F, const int n)
  {
    for (int i = 0; i < n; ++i)
    {
      F[i].vertex[0] = "";
      F[i].vertex[1] = "";
      F[i].weight = graph::INFINITE;
    }
  }

  void mergesort2(set_of_edges &data, int low, int high)
  // Problem: Sort n keys in nondecreasing sequence.
  // Inputs: positive integer n, array of key S indexed from 1 to n.
  // the array S containing the keys in nondecreasing order.
  {
    int mid;

    if (low < high)
    {
      mid = (low + high) / 2;
      mergesort2(data, low, mid);
      mergesort2(data, mid + 1, high);
      merge2(data, low, mid, high);
    }
  }

  void merge2(set_of_edges &data, int low, int mid, int high)
  {
    int i, j, k;
    // A local array needed for the merging
    set_of_edges temp = new edge[(high - low) + 1];

    i = low;
    j = mid + 1;
    k = 0;
    while (i <= mid && j <= high)
    {
      if (data[i].weight < data[j].weight)
        temp[k] = data[i++]; // Copy from first half
      else
        temp[k] = data[j++]; // Copy from second half
      k++;
    }

    // Copy any remaining entries in the left and right subarrays.
    if (i > mid)
    {
      while (j <= high)
        temp[k++] = data[j++];
    }
    else
    {
      while (i <= mid)
        temp[k++] = data[i++];
    }

    // Copy from temp back to the data array, and release temp's memory.
    i = low;
    for (k = 0; k < (high - low) + 1; ++k)
      data[i++] = temp[k];

    delete[] temp;
  }
} // namespace algorithms
// File: minspantree.cpp
#include <iostream>
#include <cstdlib>       // Provides EXIT_SUCCESS;
#include <iomanip>       // Provides setw
#include "graph.h"       // Provides graph
#include "kruskal.h"     // Provides Kruskal's algorithm
#include "disjointset.h" // Provides disjoint set
using namespace std;
using namespace data_structures;
using namespace algorithms;

int main()
{
  const int GRAPH_SIZE = 5;

  int num_of_edges = 0;
  set_of_edges E, F;

  graph example(GRAPH_SIZE);
  example.set_vertex("V1");
  example.set_vertex("V2");
  example.set_vertex("V3");
  example.set_vertex("V4");
  example.set_vertex("V5");
  example.set_edge(1, 2, 1);
  example.set_edge(1, 3, 3);
  example.set_edge(2, 1, 1);
  example.set_edge(2, 3, 3);
  example.set_edge(2, 4, 6);
  example.set_edge(3, 1, 3);
  example.set_edge(3, 2, 3);
  example.set_edge(3, 4, 4);
  example.set_edge(3, 5, 2);
  example.set_edge(4, 2, 6);
  example.set_edge(4, 3, 4);
  example.set_edge(4, 5, 5);
  example.set_edge(5, 3, 2);
  example.set_edge(5, 4, 5);

  E = new edge[GRAPH_SIZE * GRAPH_SIZE];
  make_edgeset(example, E, num_of_edges); // Copy edges from graph

  F = new edge[num_of_edges];
  init_edgeset(F, num_of_edges);

  for (int i = 0; i < num_of_edges; ++i)
    cout << "V" << E[i].vertex[0] << " to "
       << "V" << E[i].vertex[1] << " with weight " << E[i].weight << endl;

  kruskal(example.get_size(), num_of_edges, E, F); // Kruskal algorithm

  for (int i = 0; i < num_of_edges; ++i)
  {
    if (F[i].weight != 0 && F[i].weight != graph::INFINITE)
    {
      cout << setw(7) << "From" << setw(3) << "V" << F[i].vertex[0] << setw(3)
           << "to" << setw(3) << "V" << F[i].vertex[1]
           << ": " << F[i].weight << endl;
    }
  }

  delete[](E);
  delete[](F);
  return EXIT_SUCCESS;
}


Time Complexity Analysis

Basic operation

  • A comparison instruction.

Input size

  • n, the number of vertices, and m, the number of edges.

Worst-Case Time Complexity

  • $W(m,n) \in \Theta(n^2lgn^2) = \Theta(n^22lgn) = \Theta(n^2lgn)$
W(m)= The time to sort the edges(Mergesort) $W(m) \in \Theta(mlgn)$
W(m)= The time in the while loop $W(m) \in \Theta(mlgn)$
T(n)= The time to initialize n disjoint sets $T(n) \in \Theta(n)$


Optimality Proof

Recall that there is no guarantee that a given greedy algorithm always yields an optimal solution. One must prove whether or not this is the case. We will prove that Kruskal’s algorithms always produce minimum spanning trees. We show that the following proposition P is true by induction.

proposition P If F is the set of edges chosen at any stage of the algorithm, then there is some minimum spanning tree that contains F.

F가 알고리즘의 어느 단계에서 선택된 이음선의 집합이라면 F를 포함하는 최소신장트리가 존재한다.

  • Clearly P is true at the beginning, when F is empty: any minimum spanning tree will do, and there exists one because a weighted connected graph always has a minimum spanning tree.

처음 시작은 F가 공집합인 경우다. 연결되고, 가중치가 있는 비방향성 그래프에서는 항상 최소신장트리가 존재하므로, 공집합 F를 포함하는 최소신장트리가 존재한다. 따라서 명제 P는 참이다.

  • Now assume P is true for some non-final edge set F and let T be a minimum spanning tree that contains F.

P가 공집합이 아닌 이음선 집합 F에 대해서도 참이며, T가 F를 포함하는 최소신장트리라고 가정한다.

Case 1 If the next chosen edge e is also in T, then P is true for F U {e}.

다음에 선택된 이음선 e가 e ∈ T라면, F U {e}에 대해 명제 P가 참이다.

Case 2 Otherwise, e is not in T, and T U {e} has a cycle C and there is another edge e’ that is in C but not F. (Since if all the e’ are in the F, then the algorithm won’t choose e, otherwise it will be a cycle.) (If there was no such edge e’, then e could not have been added to F, since doing so would have created the cycle C.) Then T − {e’} U {e} is a tree, and it has the same weight as T, since T has minimum weight and the weight of e’ cannot be less than the weight of e, otherwise the algorithm would have chosen e’ instead of e. So T − {e’} U {e} is a minimum spanning tree containing F U {e} and again P holds.

[A graph illustrating the proof]

만일 e ∉ T라면 T U {e}는 순환경로 C를 가지며 그 순환경로상에는 F에 속하지 않은 이음선 e’가 있다.
(모든 e’가 F에 속하게 되면 알고리즘은 e를 선택하지 않는다. e를 선택하는 순간 순환경로가 생기기 때문이다.)
(그런 이음선 e’가 없다면, e를 F에 추가할 수 없다. e를 추가하면 순환경로 C가 생성되기 때문이다.)

그러면 T - {e’} U {e}는 트리이고 T와 동일한 가중치를 가진다. (T는 최소가중치를 가지며 e’의 가중치는 e의 가중치보다 작을 수 없다. 그렇지 않으면 크러스컬 알고리즘은 e대신 e’를 선택하게 된다.) 따라서 T - {e’} U {e}는 F U {e}를 포함하는 최소신장트리이며 명제 P가 유지된다.

Therefore, by the principle of induction, P holds when F has become a spanning tree, which is only possible if F is a minimum spanning tree itself.

그러므로 귀납법 원리에 의해, 명제 P(F가 알고리즘의 어느 단계에서 선택된 이음선의 집합이라면 F를 포함하는 최소신장트리가 존재)는 F가 신장트리가 될 때 성립하며, 이는 F가 최소신장트리 자체인 경우에만 가능하다.

Share